Dipole Bass Systems
26 October 2018
 Dipole
subwoofers are quite different to the other subwoofer systems described on this site
because of the way they treat the the driver's output. Your typical subwoofer driver
produces sound from both the front and the rear of the cone, and the output from the
rear is out of phase with the output from the front, which results in very reduced
response levels, unless the rear wave is treated in some fashion. The other
subwoofer systems described on this site all employ some means of dealing with
the driver's rear radiation to improve overall low frequency response, the result being a
"monopole" bass system that theoretically has the same response
characteristics in all directions. However, for dipole bass systems, the rear radiation is
left untreated, and instead the overall response of the system is adjusted by varying the
size of the baffle and the "Q" of the system to achieve the best overall
response characteristics.
Dipole
subwoofers are quite different to the other subwoofer systems described on this site
because of the way they treat the the driver's output. Your typical subwoofer driver
produces sound from both the front and the rear of the cone, and the output from the
rear is out of phase with the output from the front, which results in very reduced
response levels, unless the rear wave is treated in some fashion. The other
subwoofer systems described on this site all employ some means of dealing with
the driver's rear radiation to improve overall low frequency response, the result being a
"monopole" bass system that theoretically has the same response
characteristics in all directions. However, for dipole bass systems, the rear radiation is
left untreated, and instead the overall response of the system is adjusted by varying the
size of the baffle and the "Q" of the system to achieve the best overall
response characteristics.
Driver Characteristics
The drivers used in dipole systems tend to be quite different to those in
"monopole" bass systems. The driver's Qts tends to be particularly high
(in some cases, as high as 2.0), the idea being to introduce a "bump" in the
driver's frequency response around Fs that will compensate for the 6dB/oct rolloff in the
response that will occur when the driver is mounted in an open baffle.
Alternatively, a "normal" driver can be used in a dipole bass system, but a
considerable amount of equalization may have to be used to make up for the loss in low
frequency performance.
Response Characteristics
A dipole bass system has a "figure of eight" response pattern, which is
entirely different to the "spherical" response pattern of your typical
"monopole" subwoofer. The system's output is most powerful directly in
front and behind the baffle, and decreases to zero at the sides, where the front and rear
waveforms cancel each other. This response characteristic is said to be one of the major
advantages of a dipole bass system, as the restricted dispersion results in fewer boundary
reflections, which in turn is supposed to result in a smoother in-room response.
Drawbacks
Dipole bass systems tend to be rather large, employing multiple drivers,
primarily to make up for the output reduction due to the 6dB/oct baffle loss. This is not
the type of system to use if you've got a small living room, and it's certainly not
suitable for car audio!
Baffle Size
The response of the system will be affected by a 6dB/oct drop in output below a
particular frequency referred to as Fequal, that's directly dependent on the size of
the baffle. At Fequal, the magnitude response (SPL) of the baffled driver will be
the same as its infinite baffle response. Above Fequal, the response will rise to a 6dB
peak at Fpeak (approximately equal to 3*Fequal), and at higher frequencies, the
response will depend largely on the shape of the baffle. A completely circular
baffle will produce the worse response characteristics, with deep nulls at multiples of
Fpeak.
The following table demonstrates the relation between the baffle's effective diameter (i.e. the diameter of a circular baffle that has the same radius as the smallest dimension of the baffle), Fpeak, and Fequal:
| Speed of sound, c=344 m/s | ||
| Diameter (metres) | Fp (Hz) | Fe (Hz) |
| 0.43 | 800 | 267 |
| 0.57 | 600 | 200 |
| 1.15 | 300 | 100 |
| 1.43 | 240 | 80 |
| 1.56 | 220 | 73 |
| 1.72 | 200 | 67 |
From the table, it's plain to see that it's nearly impossible to push Fequal much lower than 80 Hz unless a fairly large baffle is used. The tradeoff here is efficiency; the smaller the baffle, the lower the final efficiency of the dipole system. OTOH, the larger the baffle, the higher the efficiency, but response at the upper end of the passband could get somewhat irregular as Fpeak is reduced.
Almost all dipole bass designs incorporate some means of boosting the response at low frequencies to compensate for the baffle loss. Typically one or more of the following methods are used:
- A high-Q driver is employed (the high Q results in a peak in the driver's free-air response at its resonance frequency).
- The Q of the system is increased by employing a series resistor (Qes is increased, which results in an increase in Qts).
- Active equalization is used to boost the low frequency response.
- Active or line-level filtering is used to cut the higher frequency levels to match the low frequency response.
Let's say we want to build a dipole bass system using four 12" drivers with the following specifications: Vas: 164 litres., Fs=30Hz, Qts=1.10, Qes=1.30, Qms=7.0, R=8 ohms, Xmax=8mm, Sd=0.0547m^2 .
To maximize efficiency, the drivers will be wired in parallel, giving an effective Re of 2 ohms. We also want to know what SPL levels we can expect if we drive the system with 100W of power.
We decide to use a baffle with an effective diameter of 1.35m.
From this, Fpeak and Fequal can be calculated:
Fpeak = c/(D)
Fpeak = 344/1.35
Fpeak = 255 Hz
Fequal = Fpeak/3
Fequal = 255/3
Fequal = 85 Hz
We can model the baffle loss by using a spreadsheet that I put together for the purpose, called dipole.xls. The spreadsheet's simulation is accurate enough for our use below Fpeak. Above Fpeak, the response of the system is greatly influenced by the shape of the baffle, so no attempt is made here to include it in the simulation.
Below is shown the estimated response curve for the given driver mounted in the stated baffle:
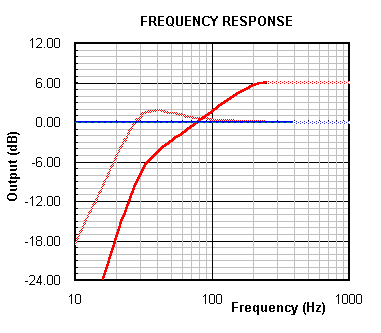
To compensate for the 6dB/oct rollof, we select to do two things: increase the Qts of the system to 1.75 to flatten the low end response, and use a line-level or active 18dB/oct LP filter at around 80Hz to reduce the high frequency response.
The effect of the increase in Qts can be seen in the graph below:

The graph below illustrates the effects of an 78Hz 18dB/oct filter on the response:

As can be seen from the graph above, the increase in Qts and the addition of the filter will produce an on-axis frequency response that extends from 28Hz to 90Hz, 0,-3dB.
To increase the Qts to the target value, we can use a series resistor Rs, and calculate its value as follows:
Qes'=Qts'*Qms/(Qms-Qts')
Qes' = 1.75*7/(7-1.75)
Qes' = 12.25/5.25
Qes' = 2.33Rs = Re*(Qes'-Qes)/Qes
Rs = 2*(2.33-1.30)/1.30
Rs = 2*1.03/1.30
Rs = 1.6 ohms
As we plan to drive the system with 100W of power, assuming 10:1 differences between average and peak levels, we can use a 10W or greater resistor for Rs.
As the total resistance, Rs+Re, will be 3.6 ohms, the amplifier will have to be capable of driving at least a 3.6 ohm load. There will also be an efficiency gain as we're using 4 drivers, and an efficiency loss because of the baffle loss and the filtering. These need to be taken into consideration when working out the final efficiency of the system.
Efficiency
We are using FOUR of these drivers in parallel. By using four
drivers this way, the resulting efficiency will be 12dB higher than the
reference efficiency for one driver. However, there will be some insertion
loss because of the use of a resistor to increase Qts. In this case,
dipole.xls predicts that the efficiency will be reduced by about 2.6dB.
Related Links:
Special thanks to the following for corrections, links and other assistance with this page:
Claude Dickson
John L. Murphy
Further References:
- R.J Newman, "Dipole Radiator Systems", JAES Jan/Feb 1980
- Linkwitz Lab - Models for a dipole loudspeaker design